I’ve recently started using NeoFly to add some economic and flight-monitoring realism to 737 flights in FS2020. NeoFly provides a simulated economy, where you can accept transit jobs between specified airports, set up hubs, pay for fuel and maintenance, earn reputation and clients, and so on. My virtual airline — Aurora Transit — mostly serves the US/Canada border region, with planned expansion to Alaska, the Aelutians, and Iceland.
I had just finished up a flight from Seattle to Philadelphia (not currently a hub for us, but a popular destination), and went to the NeoFly window to set up the next leg to our eastern Canadian hub, in Moncton.
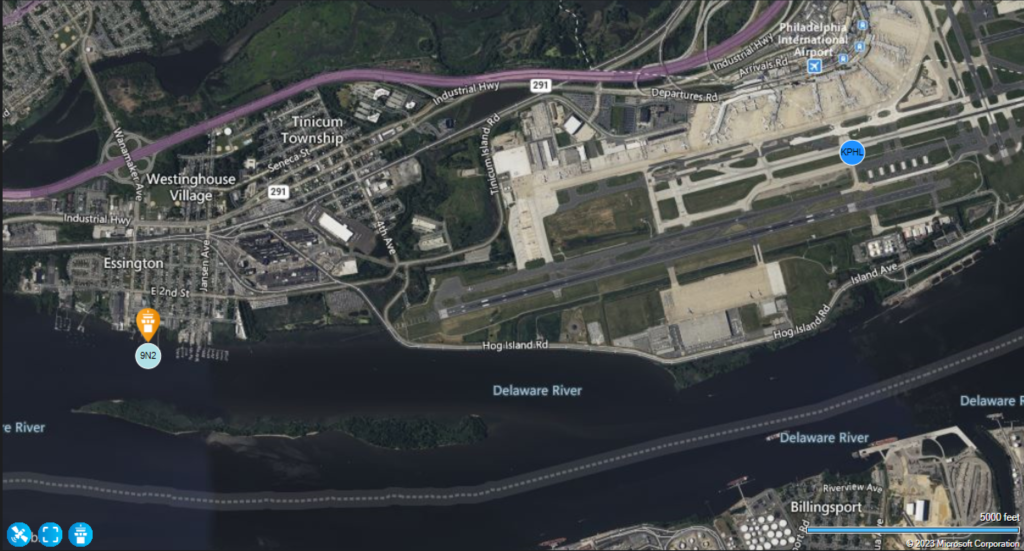
The jobs available looked a little off — and I soon realized that this was because it thought my plane was at airport “9N2” instead of Philadelphia (KPHL). Had I landed at the wrong airport, by mistake? No; Philadelphia is unmistakable from the air on a nice day like today, and we had just landed (using ILS autoland, no less!) on runway 9R, which is definitely part of KPHL.
Curious, I went to look up this “9N2” airport, and found out that it’s a seaplane base, just west of KPHL. I pulled up the Neofly planner map, and it didn’t take long to figure out the problem.
The white rectangles 1000′ from the left end of the runway mark the touchdown zone.
The symbols 9N2 and KPHL on the map represent the (single geometric point) locations that NeoFly has for those two airports. And the approach end of 9R (which is where the plane touches down, if all goes well) is actually closer to the 9N2 marker than it is to the KPHL one. So it must have thought I landed in the Delaware!
New company policy: When landing east at KPHL, we need 9L and not 9R. Or, land long!!




