Often, in embedded systems design, it is useful to be able to produce musical notes. A device which uses a brief, pleasant melody to announce an end-of-cycle condition, for example, can be perceived as more sophisticated — and therefore, more desirable — than one which simply beeps.
Musical notes can be produced by even the simplest microcontrollers, given a basic understanding of elementary music theory. Notes are distinguished by three qualities: frequency, amplitude, and timbre. Frequency is simply how many cycles per second are present — the “pitch” of the note. Amplitude is the loudness or energy present in the note. Finally, timbre is the quality of note (its shape, as seen on an oscilloscope). Sine waves are pure tones of a single frequency. Notes with other timbres have other, higher frequencies as additional components of their waveform.
Frequency is what makes a particular note, for example, a “C#” or an “E.” Higher-pitched notes are higher in frequency — and the notes are related by a specific formula. “Concert pitch A” (A4 in musical notation) is defined as 440Hz, or 440 cycles per second. Other notes, using the equal-tempered scale common in Western music, are defined from A440 using a specific formula.
This formula involves counting the number of musical half-steps (A to A#, A# to B, B to C, etc) between A440 and the note in question. The frequency of the new note is then defined by the following formula:
F = 440 * 2^(N/12)
…where N is the number of half-steps (positive or negative) between A440 and the new note. For example, A220 (one octave lower) is twelve half-steps down. Therefore:
F_A3 = 440 * 2^(-12/12)
= 440 * 2^(-1)
= 440 * 1/2
= 220Hz
This provides a good check of the formula, since each octave higher corresponds exactly to a doubling of frequency. (That’s why, musically, each note sounds similar to the same letter note one octave higher or lower.)
Once you have determined the frequency for a certain note, this is converted into a time period between half-cycles. For example, the 220Hz note in the example above would correspond to 1/220th of a second for a whole cycle, and 1/440th of a second for each half cycle. Doing the division results in a delay of 2.273 milliseconds for each half cycle. So, to produce a 220Hz “A,” a microcontroller program could do the following:
- Drive the output pin high
- Wait for 2.273 milliseconds
- Drive the output pin low
- Wait for another 2.273 milliseconds
- Repeat as desired until the tone should no longer sound.
One important consideration when producing musical notes is frequency accuracy. For a note to sound correct, its frequency should be within roughly ten “cents” of the correct tone (where 100 “cents” is equal to the frequency ratio of one musical half-step.) For an ideal note frequency of 220Hz (corresponding to A3), this means the actual frequency of the note must be between 218.73Hz and 221.27Hz. The delay for each half-cycle, therefore, must be between roughly 2.260ms and 2.286ms. (A delay of 2.273ms would be nearly ideal.)
Here is a list of the ideal frequencies for each note in the range from C3 (one octave below Middle C) to C5 (one octave above Middle C), along with the minimum and maximum acceptable frequencies and the corresponding minimum and maximum half-cycle delay times, assuming an allowed tolerance of ten cents. For higher octaves, double the frequencies and divide the delay times by two. For lower octaves, divide the frequencies by two and double the delay times.
(Here is the original Excel file, with formulas.)

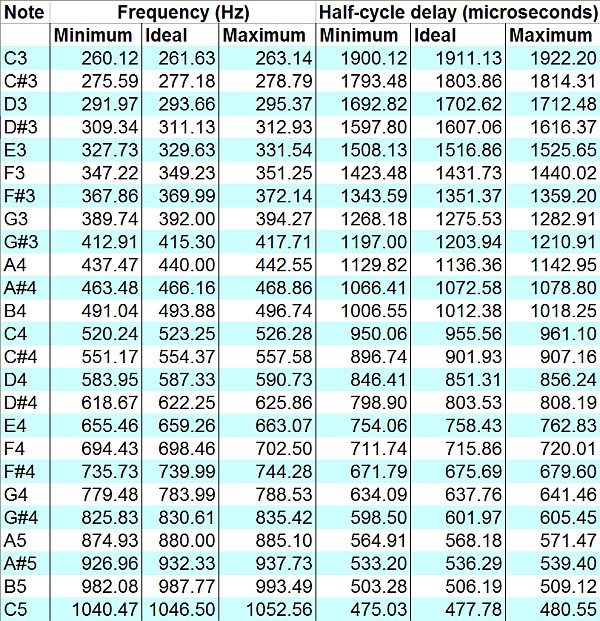

What ‘s the chart used for? I dont see the number “2.273 milliseconds” in this chart 🙁 Iam not good at English :”>
The chart shows the frequencies for the notes. A220 in the example is too low a note to be on the chart. A440 is similar, but with double the frequency, so half the cycle times (1.136 milliseconds instead of 2.273ms.)
(Also, the times in the chart are in microseconds. 1ms = 1000us.)
Your English seems very good to me. (Va toi khong noi tieng Viet gioi.):-)